Subiectul I. 1
Rezultatul calculului 16-16:4 este egal cu … .
Pasul 1.
Efectuez întâi operația de gradul 2, împărțirea: 16-16:4=16-4
Pasul 2.
Efectuez scăderea rămasă: 6-16:4=16-4=12
Subiectul I. 2
Dacă \(frac{x}{10}=\frac{20}{100}\), atunci numărul x este egal cu … .
Înmulțesc cu 10 ecuația și obțin: x=\(\frac{10\cdot 20}{100}\)=2
Subiectul I.3
Numărul natural din intervalul (0,2) este egal cu … .
Toate numerele din interval sunt strict mai mari decât \(0\) și strict mai mici decât 2.
Singurul număr natural \(n\) pentru care\[\text{0 }<\text{ }n\text{ }<\text{ }2\] este \(1\).
Subiectul I.4
Rombul ABCD are diagonalele AC=16 cm și \(BD=12 cm\). Lungimea laturii AB a acestui romb este egală cu … cm.
Pasul 1. Fie \(O\) intersecția diagonalelor. Deoarece într-un romb diagonalele se taie în jumătate, avem: \[AO=AC:2=8\,cm\] și \[BO=BD:2=6\,cm\]
Pasul 2. Într-un romb, diagonalele sunt perpendiculare, deci \(AOB\) este dreptunghic în \(O\)
Aplic teorema lui Pitagora în triunghiul \(AOB\):\[A{{B}^{2}}=A{{O}^{2}}+B{{O}^{2}}={{8}^{2}}+\,{{6}^{2}}=100\,cm\]. Deci \[AB=10\,cm\]
Subiectul I.5
Secțiunea axială a cilindrului circular drept reprezentat în Figura 1 este un pătrat cu latura de \(6\,cm\). Volumul acestui cilindru este egal cu …\(\pi \,c{{m}^{3}}\)
Pasul 1. Latura pătratului este diametrul bazei cilindrului, deci raza bazei este: \[r=6:2=3\,cm\]
Pasul 2. Aria bazei este: \[{{A}_{b}}=\pi {{r}^{2}}=9\pi \,c{{m}^{2}}\]
Pasul 3. Înălțimea cilindrului, \(h\), este latura pătratului
Volumul este: \[V={{A}_{b}}\cdot h=54\pi \,c{{m}^{3}}\]
Nota la teză 1 2 3 4 5 6 7 8 9 10
Număr de elevi 0 0 1 2 3 4 5 6 5 3
Subiectul I. 6
În tabelul de mai jos este prezentată repartiția elevilor unei clase a VIII-a, în funcție de notele obținute la teza la matematică, în semestrul al II-lea.
| Nota la teză | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Număr de elevi | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 5 | 3 |
Conform tabelului numărul elevilor care au obținut la teză cel puțin nota 9 este mai mare decât numărul elevilor care au obținut la teză cel mult nota 4 cu … .
Pasul 1. Elevii care au luat cel puțin \(9\) sunt cei care au luat \(9\) și \(10\). Numărul lor este \[5+3=8\]
Pasul 2. Elevii care au luat cel mult \(4\). sunt cei care au luat \(1\)., \(2\)., \(3\). și \(4\).. Numărul lor este\[0+0+1+2=3\]
Pasul 3. Diferența dintre cele două numere este \[8-3=5\]
Subiectul II. 1
Desenați, pe foaia de examen, o piramidă patrulateră de vârf V și bază ABCD.
Pasul 1. Construim baza piramidei pe care, deși este pătrat, o desenăm ca pe un paralelogram. Apoi îi trasăm diagonalele
Pasul 2. Prin punctul de intersecție al diagonalelor construim perpendiculara pe planul bazei
Pasul 3. Unim capătul înălțimii, care nu aparține planului bazei, cu vârfurile bazei și obținem o piramidă patrulateră regulată
Pasul 4. Notăm cu V, vârful piramidei și baza cu ABCD
Subiectul II. 2
Arătați că suma numerelor \(x=\left( \sqrt{2}+\frac{5}{\sqrt{2}} \right)\cdot \sqrt{2}-\left( \sqrt{3}+\frac{1}{\sqrt{3}} \right)\cdot \sqrt{3}\)și \(y=\left( \frac{3}{2\sqrt{5}}+\frac{2}{3\sqrt{5}} \right):\frac{1}{\sqrt{180}}\)este pătratul unui număr natural.
Pasul 1. Calculez \(x\): \(x=\left( \sqrt{2}+\frac{5}{\sqrt{2}} \right)\cdot \sqrt{2}-\left( \sqrt{3}+\frac{1}{\sqrt{3}} \right)\cdot \sqrt{3}=\left( 2+5 \right)-\left( 3+1 \right)=7-4=3\)
Pasul 2. Calculez \(y\): \(y=\left( \frac{3}{2\sqrt{5}}+\frac{2}{3\sqrt{5}} \right):\frac{1}{\sqrt{180}}=\left( \frac{3}{2\sqrt{5}}+\frac{2}{3\sqrt{5}} \right):\frac{1}{6\sqrt{5}}=\left( \frac{3}{2\sqrt{5}}+\frac{2}{3\sqrt{5}} \right)\cdot 6\sqrt{5}=3\cdot 3+2\cdot 2=13\)
Pasul 3. Calculez suma lor: \[x+y=3+13=16={{4}^{2}}\]
Subiectul II. 3
Perimetrul unui dreptunghi este egal cu 220 cm. Determinați lungimea și lățimea acestui dreptunghi, știind că, dacă am mări lățimea dreptunghiului cu 10 cm și am micșora lungimea dreptunghiului cu 20 cm, am obține un dreptunghi cu aria egală cu aria dreptunghiului inițial.
Pasul 1. Notez lungimea cu \(L\) și lățimea cu \(l\). Perimetrul este egal cu \[2l+2L\], deci \[220=2l+2L\], rezultă \[l=110-L\]
Pasul 2. Aria dreptunghiului inițial este\(l\cdot L\). Aria dreptunghiului obținut după modificările din enunț este (\[(l+10)\cdot (L-20)\]. Cele două sunt egale. \[l\cdot L=(l+10)(L-20)\]
Pasul 3. Înlocuiesc \(l\) cu \[110-L\] în ecuația obținută din egalitatea celor două arii. \[(110-L)\cdot L=(110-L+10)(L-20)\] \[(110-L)\cdot L=(120-L)(L-20)\], adică \[110L-{{L}^{2}}=120L-2400-{{L}^{2}}+20L\]. Obțin: \[30L=2400\] deci \[L=80\,cm\] și \[l=110-80=30\,cm.\]
Subiectul II. 4. a.
Se consideră funcția \(f:\mathbb{R}->\mathbb{R},\text{ }f(x)=3x+1\).
Pasul 1. Pentru a putea reprezenta grafic funcția trebuie să determin două puncte de pe reprezentarea sa grafică. Determin primul punct.
\(f(0)=3\cdot 0+1=1\)Am obținut punctul
\(A\left( 0,1 \right)\)Pasul 2. Determin cel de-al doilea punct de pe reprezentarea grafică a funcției.
\(f(1)=3\cdot 1+1=4\)Am obținut punctul
\(B(1,4)\)Pasul 3. Reprezint punctele determinate la pașii anteriori într-un sistem de axe ortogonale, le unesc și trasez dreapta care este reprezentarea grafică a funcției.
Subiectul II. 4. b.
Se consideră funcția \(f:\mathbb{R}->\mathbb{R},\text{ }f(x)=3x+1\)
Pasul 1. Fie \(C\) punctul de coordonate \((0,4)\)
Triunghiul \(ABC\) este dreptunghic în\(C\) pentru că \(AC\) este pe axa\(Oy\), iar \(C\) și \(B\) au ambele \[y=4\], deci \(BC\) este paralelă cu\(Ox\). Înseamnă că \[tg\left( \sphericalangle BAC \right)=\frac{BC}{AC}=1:3=0,\left( 3 \right)\] Cum \(BAC\) este unghiul format de graficul lui \(f\) cu axa \(Oy\), răspunsul este \[0,\left( 3 \right)\]
Subiectul II. 5
Se consideră expresia \(E\left( x \right)=~\left( \frac{x}{x+2}-\frac{3}{2-x}-\frac{6x}{{{x}^{2}}-4} \right):\frac{{{\left( x-2 \right)}^{2}}-1}{{{x}^{2}}+x-2}\)unde x este număr real, \(x\ne -2,~~x\ne 1,~~x\ne 2\) și x=3. Arătați că \(E\left( x \right)\text{ }=\text{ }1\) pentru orice x număr real, \(x\ne -2,~~x\ne 1,~~x\ne 2\) și x=3
Pasul 1. Calculez paranteza, aducând la același numitor
\(\frac{x}{x+2}-\frac{3}{2-x}-\frac{6x}{{{x}^{2}}-4}=\frac{x(x-2)}{{{x}^{2}}-4}+\frac{3(x+2)}{{{x}^{2}}-4}-\frac{6x}{{{x}^{2}}-4}=\) \(=\frac{{{x}^{2}}-2x+3x+6-6x}{{{x}^{2}}-4}=\frac{{{x}^{2}}-5x+6}{{{x}^{2}}-4}=\frac{\left( x-2 \right)(x-3)}{\left( x-2 \right)(x+2)}=\frac{x-3}{x+2}\)Pasul 2. Simplific fracția la care se împarte paranteza
\(\frac{{{\left( x-2 \right)}^{2}}-1}{{{x}^{2}}+x-2}=\frac{{{x}^{2}}-4x+3}{{{x}^{2}}+x-2}=\frac{\left( x-1 \right)(x-3)}{\left( x+2 \right)(x-1)}=\frac{x-3}{x+2}\)Pasul 3. Înlocuiesc rezultatele obținute la pașii anteriori și calculez expresia \(E(x)\)
\(E\left( x \right)=\frac{x-3}{x+2}:\frac{x-3}{x+2}=1\)Subiectul III. 1.a.
În Figura 2 este reprezentat un dreptunghi \(ABCD\) cu \(AB>CD\) și\(AC=4\,dm\), iar punctul \(O\) este intersecția diagonaleleor dreptunghiului. Punctele\(E\) și \(F\) sunt mijloacele segmentelor \(AO\), respectiv CO și punctul L aparține laturii AB, astfel încât \(LE=LF\)
Într-un dreptunghi, diagonalele se taie în jumătate, deci\[AO=OC\]. Știu că \(OE\) este jumătate din \(AO\), deci \[OE=AO:2=(AC:2):2=(4:2):2=1\,dm\]
Subiectul III. 1.b.
În Figura 2 este reprezentat un dreptunghi \(ABCD\) cu \(AB>CD\) și\(AC=4\,dm\), iar punctul \(O\) este intersecția diagonaleleor dreptunghiului. Punctele\(E\) și \(F\) sunt mijloacele segmentelor \(AO\), respectiv\(CO\) și punctul \(L\) aparține laturii \(AB\), astfel încât \(LE=LF\).
OL este mediană în triunghiul ELF și EL=LF, deci OL este și înălțime. Rezultă că \[m(\sphericalangle AOL)={{90}^{\circ }}=m(\sphericalangle ABC)\]. Triunghiurile \[AOL\]și\(ABC\)au unghiul \(BAC\) comun și \(m(\sphericalangle AOL)=m(\sphericalangle ABC)\). Folosind cazul de asemănare unghi-unghi, rezultă că cele două triunghiuri sunt asemenea.
Subiectul III. 1.c.
În Figura 2 este reprezentat un dreptunghi \(ABCD\) cu \(AB>CD\) și\(AC=4\,dm\), iar punctul \(O\) este intersecția diagonaleleor dreptunghiului. Punctele\(E\) și \(F\) sunt mijloacele segmentelor \(AO\), respectiv\(CO\) și punctul \(L\) aparține laturii \(AB\), astfel încât \(LE=LF\)
Pasul 1. Observ că \[EF=AC:2\]. Triunghiul \[LEF\]este echilateral și \(OL\) este înălțimea lui. Rezultă că: \[OL=EF\sqrt{3}:2=AC:2\cdot \sqrt{3}:2=4:2\cdot \sqrt{3}:2=\sqrt{3}dm\]
Pasul 2. Din asemănarea triunghiurilor \(AOL\) și \(ABC\)rezultă că \(\frac{AO}{OL}=\frac{AB}{BC}\). Deci: \(BC=\frac{AB\cdot OL}{AO}=\frac{AB\sqrt{3}}{2}\)
Pasul 3. Aplic teorema lui Pitagora în triunghiul \(ABC\): \[A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}=A{{B}^{2}}+A{{B}^{2}}\cdot 3:4=A{{B}^{2}}\cdot 7:4\]. Rezultă:\[A{{B}^{2}}=\frac{4A{{C}^{2}}}{7}=\frac{64}{7}\], deci: \[AB=\frac{8\sqrt{7}}{7}dm\]
Subiectul III. 2.a.
În Figura 3 este reprezentat un tetraedru regulat ABCD cu AB=10 cm. Punctele M și N sunt mijloacele muchiilor CD, respectiv BC.
Un tetraedru are 6 muchii. Deoarece\(ABCD\) este regulat, toate muchiile lui sunt egale. Rezultă că suma muchiilor este: \(6\cdot AB=60\,cm\)
Subiectul III. 2.b.
În Figura 3 este reprezentat un tetraedru regulat \(ABCD\)cu\(AB=10\,cm\). Punctele \(M\) și \(N\) sunt mijloacele muchiilor \(CD\), respectiv \(BC\)
Pasul 1. O față a tetraedrului regulat este triunghi echilateral deci aria unei fețe se poate calcula cu formula \({{A}_{f}}=\frac{A{{B}^{2}}\sqrt{3}}{4}=25\sqrt{3}\,c{{m}^{2}}\)
Pasul 2. Tetraedrul are 4 fețe, toate congruente, deci aria totală este \({{A}_{t}}=4\cdot {{A}_{f}}=4\cdot 25\sqrt{3}=100\sqrt{3}\,c{{m}^{2}}=\sqrt{3}\,d{{m}^{2}}\)
Subiectul III. 2.c.
În Figura 3 este reprezentat un tetraedru regulat ABCD cu AB=10 cm. Punctele M și N sunt mijloacele muchiilor CD, respectiv BC.
Pasul 1. Fie R intersecția dreptelor MQ și BD. Notez cu O intersecția dreptelor DN și BM, adică centrul de greutate al triunghiului echilateral \[BCD\]
Cum centrul de greutate se află la două treimi de vârf și o treime de bază, rezultă că OD=2ON. Cum\[DQ=DN:3\], rezultă că\( DQ=ON\), deci \( Q\). este mijlocul lui\[OD\]. Deoarece \( MQ\) este mediană în triunghiul dreptunghic OMD, rezultă că MQ este jumătate din ipotenuza OD, adică MQ=OQ=DQ
Pasul 2. \( ND\). este bisectoara unghiului \( BDC\) deci\( m(\sphericalangle MDO)=m(\sphericalangle RDO)={{30}^{\circ }}\). Pe de altă parte, triunghiul \( MOQ\). este echilateral, deci \( m(\sphericalangle MQO)={{60}^{\circ }}\). Cum \[\sphericalangle MQO\]și \[\sphericalangle RQD\]sunt unghiuri opuse la vârf, \[m(\sphericalangle RQD)=m(\sphericalangle MQO)={{60}^{\circ }}\] Înseamnă că triunghiul \( RQD\) are \( m(\sphericalangle RDQ)={{30}^{\circ }}\) și \( m(\sphericalangle RQD)={{60}^{\circ }}\)., de unde rezultă că triunghiul \( RQD\). este dreptunghic în \( R\).
Pasul 3. Deoarece triunghiul \( RQD\). este dreptunghic în \( R\). și \( m(\sphericalangle RDQ)={{30}^{\circ }}\)., rezultă că \( QR\). este jumătate din ipotenuza \(QD\).. Dar \( QD=MQ\) deci \( MQ=2QR\).
Pasul 4. Cum \( MQ=2QR\)., rezultă \[QR>MR=1:3=AP:AM\]. Reciproca teoremei fundamentale a asemănării îmi spune că\( PQ\). este paralelă cu\( AR\) Cum \( AR\). este inclusă în planul \( (ABD) \)., iar \( PQ\) nu este inclusă în \( (ABD) \)., rezultă că \( PQ\). este paralelă cu \( (ABD) \)
Ai nevoie de ajutor la mate? Gasesti pe ExamenulTau.ro toate resursele pentru:
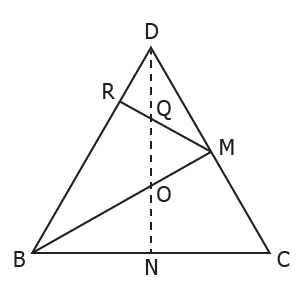
Buna ziua. In cadrul demonstrației unei probleme, se accepta prescurtări de genul T.P. sau T. Pit. sau trebuie scris T.Pitagora sau chiar Teorema lui Pitagora?
Bună, Dana! Nu aş şti să îţi zic cu exactitate, însă, dacă nu este interzis clar în regulament, nu ar trebui să fie o problemă dacă prescurtezi, atât timp cât este foarte clar la ce te referi. În acest sens, eu nu aş prescurta T.P., de exemplu 🙂 Sper că ţi-am fost de ajutor! Mult succes şi o zi frumoasă îţi doresc!