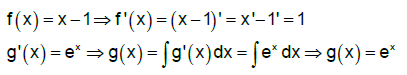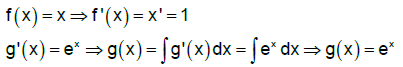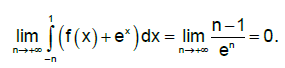Blog ExamenulTau
Log In
Become a part of our community!
Registration complete. Please check your email.
Create an account
Welcome! Register for an account
The user name or email address is not correct.
Reset password
Recover your password
Password reset email has been sent.
The email could not be sent.
Possible reason: your host may have disabled the mail function.


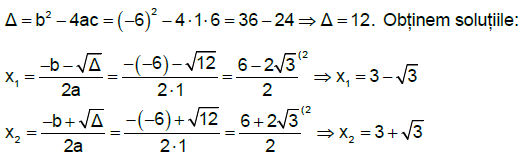
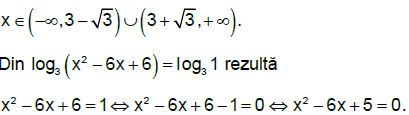
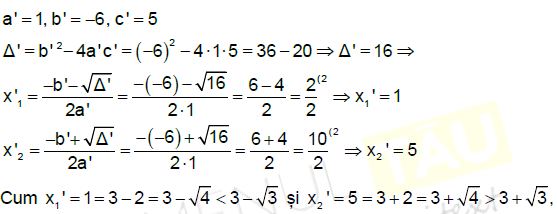 rezultă că mulțimea soluțiilor ecuației este S = {1,5}.
rezultă că mulțimea soluțiilor ecuației este S = {1,5}.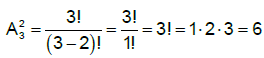 numere. În concluzie se pot forma 6 numere naturale pare, de trei cifre distincte, cu cifrele 5,7,8 și 9.
numere. În concluzie se pot forma 6 numere naturale pare, de trei cifre distincte, cu cifrele 5,7,8 și 9.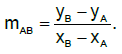 Înlocuind coordonatele punctelor A(1,0) și B(1,2), obținem
Înlocuind coordonatele punctelor A(1,0) și B(1,2), obținem 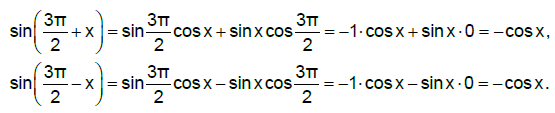
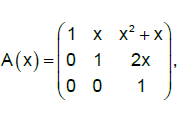 unde x este un număr real.
unde x este un număr real.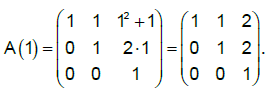
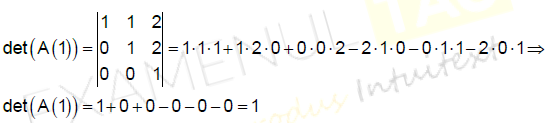
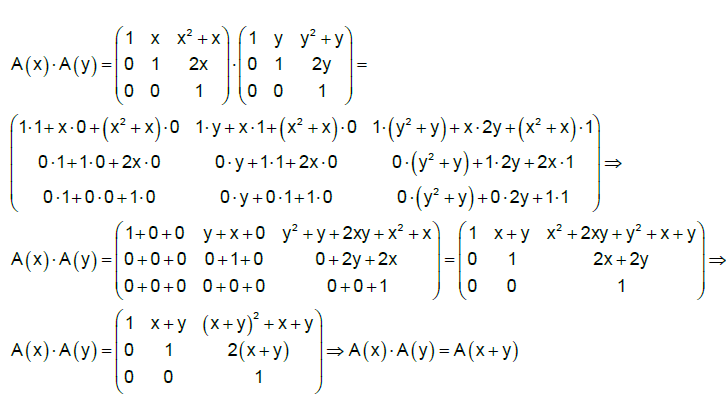
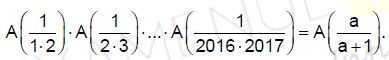

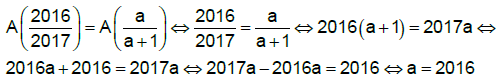
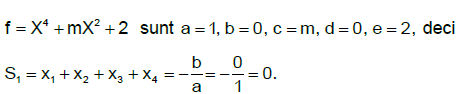
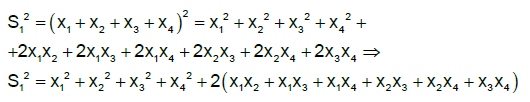
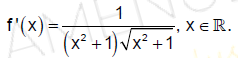

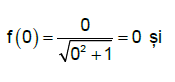
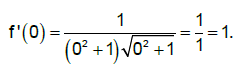
 Cum
Cum